
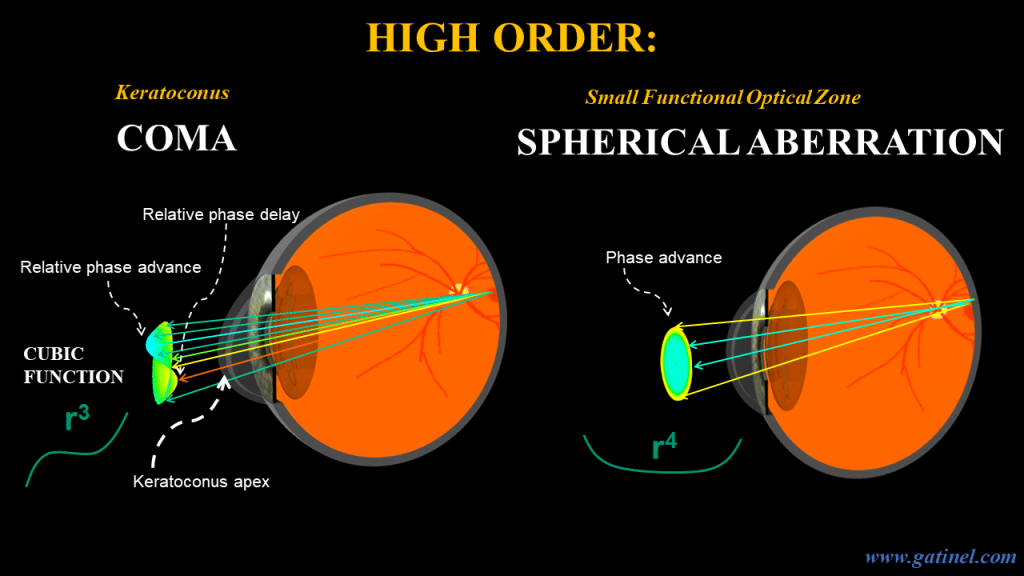
One of the most interesting points in the Zernike vector analysis was the distribution of the axes for coma and trefoil. Besides this, different scalings of the Zernike polynomials are used. For instance, Zernike term for primary coma, Z z318(33-2)cos, has the maximum value of 8z31 for 1 and 0, cos1 (i.e. Our results confirmed that coma and trefoil in keratoconic eyes were markedly higher, according to Zernike vector analysis. The Zernike and LoganShepp polynomials span the same space, that of Cartesian polynomials of a given total degree, but the former allows partial factorization whereas the latter basis facilitates an efficient algorithm for solving the Poisson equation. Figures 3(a) and 3(b) show the OPD profiles of the bare lens and LSAM, respectively, from which the OPD profile of a perfect. Where $\Im$ is the Fourier Transform function this page uses a 512-point FFT.Different orderings of the Zernike polynomials are in use. Figure 3 compares the Zernike analysis results of the lens and LSAM.
Coma x zernike series#
The wavefront is the Zernike polynomial series They were named after the optical physicist Frits Zernike (figure 1 ), winner of the 1953 Nobel Prize in Physics and the inventor of phase-contrast microscopy.
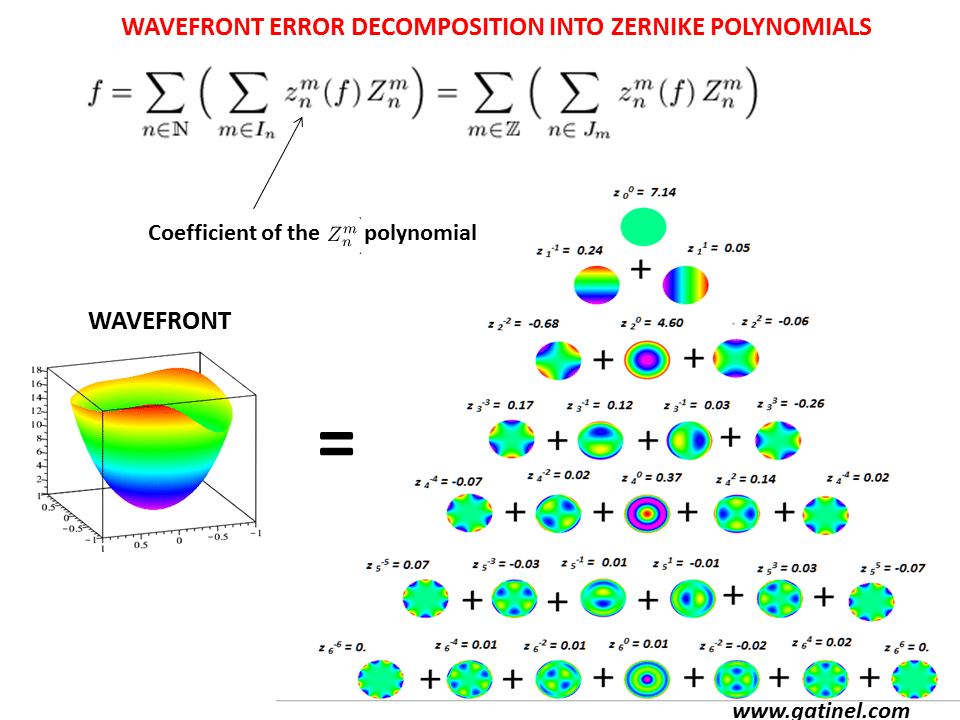
$x_p$ and $y_p$ are the normalized exit pupil coordinates, where the $x_p$ axis defines the sagittal plane and the $y_p$ axis defines the meridional plane.Įach aberration is specified using two subscripts $n$ and $m$. Zernike polynomials are just a special flavor of Jacobi polynomials. The Zernike polynomials are a sequence of continuous functions that form a complete orthogonal set over a unit disk. Optical system is assumed to be circular in shape. All wavefront data is measured in the exit pupil. The key paraxial data we need is the exit pupil position and exit pupil diameter. The conventional conversion methods convert interference fringe images to Zernike coefficients and require two steps, which are complex mathematical calculations. This page computes and plots variuos characteristics of the Zernike polynominals. We present a population study of peripheral wavefront aberrations in large off-axis angles in terms of Zernike coefficients. In order to produce a black box model, we must first produce a paraxial optical system with the same first-order properties and then aberrate the wavefront produced by this paraxial system with the Zernike data.


 0 kommentar(er)
0 kommentar(er)
